Volume Of A Spherical Cap Derivation

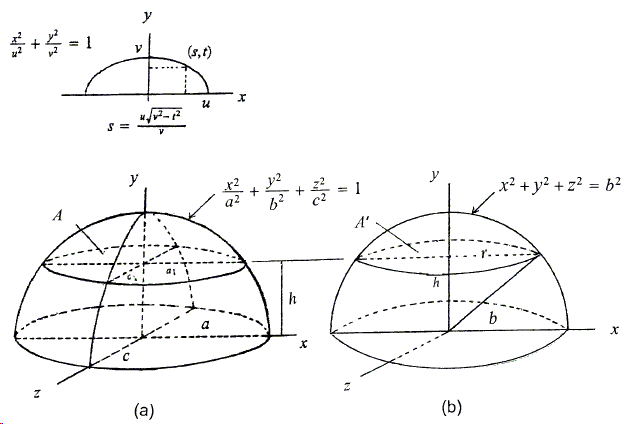
In geometry, a spherical cap or spherical dome is a portion of a sphere or of a ball cut off by a plane. It is also a spherical segment of one base, i.e., bounded by a single plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a hemisphere. In geometry, a spherical cap or spherical dome is a portion of a sphere cut off by a plane. Spherical cap In geometry, a spherical cap is a portion of a sphere cut off by a plane. If the plane passes through the center of the sphere, so that the height of the cap is equal to the radius of the sphere, the spherical cap is called a "hemisphere".

For solids of revolution, the volume slices are often disks and the cross-sections are circles. The method of disks involves applying the method of slicing in the particular case in which the cross-sections are circles, and using the formula for the area of a circle. A spherical cap is the region of a sphere which lies above a given plane. If the planepasses through the center of the sphere, the cap is a called a hemisphere, and if the cap is cut by a second plane, the spherical frustum is called a spherical segment. However, Harris and Stocker use the term "spherical segment" as a synonym for what is here called a spherical cap and "zone" for spherical segment. In geometry, a spherical sector is a portion of a sphere defined by a conical boundary with apex at the center of the sphere.

It can be described as the union of a spherical cap and the cone formed by the center of the sphere and the base of the cap. I suspect you are really asking about a spherical cap on each end of a horizontal cylindrical tank, as if taking the sphere in your picture and cutting a slice from it vertically. So for any given depth of liquid, you want the total volume of a part of a spherical cap and a partially filled cylinder . The spherical cap is the portion of a sphere that lies above a plane of the sphere. If the base area, height and the sphere radius is known then the volume can be found out of the particular portion.

Spherical dome is the term used synonymously to the spherical cap. This is summarized in the following rule. A hemisphere, as the name suggest, is one part of a sphere that is divided into two equal halves. The total surface area of each hemisphere consists of base area and cap area.

The volume of a spherical sector is 23⁢π⁢r2⁢h, where h is the height of the spherical cap of the spherical sector and r is the radius of the sphere. The total volume of a partially-filled spherical tank equals total sphere volume minus spherical cap volume. This is the figure described in the question. The sphere is there for comparison; the cylinder has had a cone drilled out from the top and the bottom, leaving solid material around it. We're going to slice both the cylinder and the sphere at a height h above the center. But for students who only know geometry, "wait until you learn calculus" can be unsatisfying.

Fortunately, there are a couple ways to do it using only geometrical ideas . The important thing is that they can be followed without deep knowledge. Enter radius of the sphere and height of the spherical cap and choose the number of decimal places. This first result for a google search for "volume of sphere proof without calculus" should work for spherical caps as well. In the following problems, students will calculate the volume of a sphere using the formula derived in the lesson. Then, students will derive the formula for the volume of a hemisphere using a similar integration technique.

Last, students will use their new formula to find the volume of a specific hemisphere. Yes; that's called a spherical cap; that is, the part of a sphere cut off by a plane at some distance from the center. "Hemispherical" in your description is irrelevant. (not the circle of which it is a part of but the cap's distance to center of the arc) which u can say is a part of the length of the tank... About 1800 years prior to the discovery of calculus, Archimedes showed that the surface area of a sphere of radius is .

He also showed that the volume of a ball of radius is using the Cavalieri's principle, again without calculus . Use spherical coordinates to find the volume of the triple integral, where ??? Also on that page you will see an explanation of the 4/3 in the volume of the sphere. In brief, you can imagine drawing a tiny triangle on the surface of the sphere and connecting its corners to the center of the sphere. The volume of a pyramid is 1/3 times the area of the base times the height.

Thus the volume of this pyramid is 1/3 times the radius of the sphere, times the area of that little triangle. Usually these volume and area formulas are derived using calculus; but they were first worked out by the Greeks, notably Archimedes, using geometrical methods. The complete proof of the formulas can be a little involved, but I can give you the basic idea. I like to start with the area of the sphere, and get the volume from that - that covers two questions at once. 56.Find the volume of a sphere of radius R[/latex] with a cap of height h[/latex] removed from the top, as seen here. If a solid of revolution has a cavity in the center, the volume slices are washers.

With the method of washers, the area of the inner circle is subtracted from the area of the outer circle before integrating. Definite integrals can be used to find the volumes of solids. Using the slicing method, we can find a volume by integrating the cross-sectional area. Solids of revolution are common in mechanical applications, such as machine parts produced by a lathe. We spend the rest of this section looking at solids of this type.

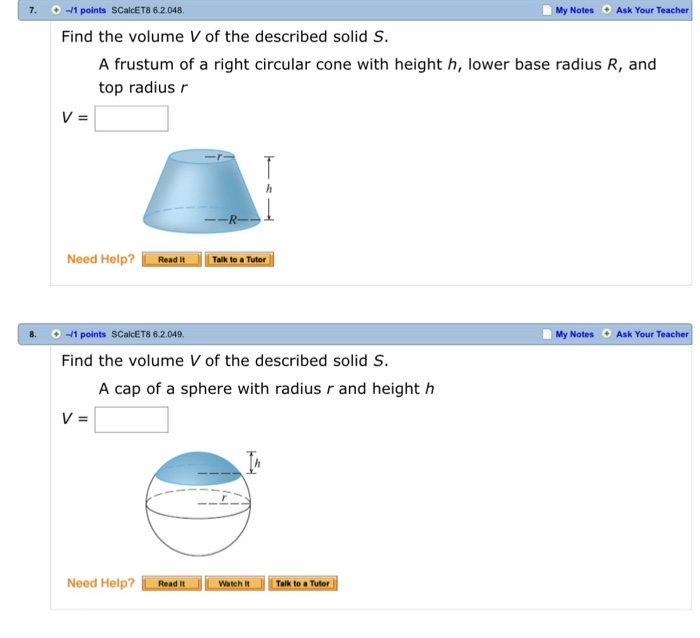
The next example uses the slicing method to calculate the volume of a solid of revolution. The spherical segment of one base is also called spherical cap and the two bases is also called spherical frustum. The bases of a spherical segment are the sections made by the parallel planes. The radii of the lower and upper sections are denoted by a and b, respectively. If either a or b is zero, the segment is of one base.

If both a and b are zero, the solid is the whole sphere. Spherical segment is a solid bounded by two parallel planes through a sphere. In terms of spherical zone, spherical segment is a solid bounded by a zone and the planes of a zone's bases.

The volume of a spherical cap is found using integrals and the method of disks used in "volume of a Solid of revolution". A thin rectangle in the region between two curves. A representative disk formed by revolving the rectangle about the x -axis . The region between the curves over the given interval.

Let us now describe how he discovered the surface area of a sphere. First, we inscribe the sphere of radius in a cylinder of the same radius and height as shown. We can use triple integrals and spherical coordinates to solve for the volume of a solid sphere. This is because the two triangles shown are similar, if slant height l is tangent to the sphere and therefore perpendicular to the radius r. The ratio \(\frac\), by the way, is the cosine of the latitude, which Randy mentioned in his question above. A representative disk formed by revolving the rectangle about the x\text.[/latex] The region between the curves over the given interval.

Some solids of revolution have cavities in the middle; they are not solid all the way to the axis of revolution. Sometimes, this is just a result of the way the region of revolution is shaped with respect to the axis of revolution. In other cases, cavities arise when the region of revolution is defined as the region between the graphs of two functions. A third way this can happen is when an axis of revolution other than the x\text[/latex] or y\text[/latex] is selected. We can also calculate the volume of a cylinder. Although most of us think of a cylinder as having a circular base, such as a soup can or a metal rod, in mathematics the word cylinder has a more general meaning.

To discuss cylinders in this more general context, we first need to define some vocabulary. In the preceding section, we used definite integrals to find the area between two curves. In this section, we use definite integrals to find volumes of three-dimensional solids. We consider three approaches—slicing, disks, and washers—for finding these volumes, depending on the characteristics of the solid. Calculates the volume and surface area of a partial sphere given the radius and height.

Use the formula derived in the previous problem to calculate the volume of a hemisphere with radius 2 inches. If one of the parallel planes is tangent to the sphere, the solid thus formed is a spherical segment of one base. Each disk has a radius of $R \sin(\theta)$, as before. Notice that one thing we can easily find is the area of a single horizontal slice of the ball. This is the shaded disk at the top of the diagram, which is drawn at height z. The disk has a radius of x, which we'll need to find the area of the disk.

To find x, we can form a right triangle with sides z and x, and hypotenuse r. The volume of a spherical cap is π⁢h2⁢(r-h3), when h is its height and r is the radius of the sphere. Sometimes in the question you will be given the base radius while in some you will be given as the sphere radius. IT important to differentiate and use the respective formula to find the surface area. Use the disk method to derive the formula for the volume of a trapezoidal cylinder.

Use the slicing method to derive the formula for the volume of a cone. A thin rectangle for approximating the area under a curve. The region under the curve is revolved about the x -axis , x -axis , resulting in the solid of revolution. The following picture is the cross section of the inscribed sphere along the plane, which then becomes a circle of radius inscribed in a square of side . I record here a remarkable discovery of Archimedes about the formula for the surface area of a sphere. I think the derivation is elementary enough so that it can be taught in high school.

My point is that many formulas taught in high school can be demonstrated in a rather natural and elementary way, which can be helpful to understand or remember them. Again, we are assuming that the pieces we use are small enough that we can treat the base of the pyramid as flat, and yet consider its height to be the radius of the sphere. Calculus, or a similar argument involving limits, is needed to make this a valid proof. 11.The base is a circle of radius a.[/latex] The slices perpendicular to the base are squares.

4.Use the disk method to derive the formula for the volume of a trapezoidal cylinder. 2.Use the slicing method to derive the formula for the volume of a cone. As with the disk method, we can also apply the washer method to solids of revolution that result from revolving a region around the y[/latex]-axis. In this case, the following rule applies. A representative disk formed by revolving the rectangle about the x\text\text[/latex] The region under the curve is revolved about the x\text,[/latex] resulting in the solid of revolution.

Find the volume of a solid of revolution using the disk method. Archimedes' hat-box theorem states that for any sphere section, its lateral surface will equal that of the cylinder with the same height as the section and the same radius of the sphere. In the question, we have to prove that the hemisphere in closes the largest volume among all this medical gaps, off fixed spectacle or surface area. So for proving these when it do do this question veggies.

We have to find real estate so he does Age equals is upon to minus private three in tow three squad, this equal do is upon to minus bye Hitch Square. So we have fine in the squad that is equal to basic on for Dubai edges squad equals on dhe. It just quiet because is upon to buy um, it's equals gaze upon to buy it that is equal. So this response to there is hence the hemisphere in closes the largest while you. Oh, fixed surface area surface idea Kiss No, the volume because one upon three into s into Uganda is upon to buy Because we have this age equals broken That is upon to buy on. We have the volume man's when the country surface area in bridge So this is the morning Sid, answer to your problem.

In this lesson, we derive the formula for finding the volume of a sphere. This formula is derived by integrating differential volume elements formed by slicing the sphere into cylinders with a differential thickness. This video explains how to use a triple integral to determine the volume of a spherical cap. I need to calculate the volume of tank as a function of height of tank.

I don't think you've stated the problem fully. At the end you mention a cylinder, which hasn't been mentioned previously; and the first pair of pictures don't match the other picture and the formulas. Also, you say that the r in the formula is the "circular radius", but it is in fact the radius of the sphere. A spherical cap is a portion of a sphere cut off by a plane.

A sphere is a solid bounded by a surface all points of which are equally distant a point within, called center. While calculus is a powerful tool, nevertheless geometrical methods can be very effective in settings where initially it might appear that calculus has an exclusive role. For example, the focusing property of the parabola can be established with a rather simple indirect proof. It is a principle of optics that when a beam of light strikes a curved mirror at a point, the light behaves as if the mirror were flat at that point.

Seen on edge, a curved mirror looks like a curved line. Light in the plane of the curve striking it at a point makes equal angles with the line which is tangent to the curve at the point. A spherical cap is defined as as a portion of the sphere cut by a plane. Derive the formula for the volume of a sphere using the slicing method.

As with the disk method, we can also apply the washer method to solids of revolution that result from revolving a region around the y-axis. Although some of these formulas were derived using geometry alone, all these formulas can be obtained by using integration. In order to find limits of integration for the triple integral, we'll say that ??? Then we only have to find an interval for ??? Take a sphere of radius R, and imagine constructing a cylindrical box with radius R and height 2R. You can see that the sphere will fit snugly inside this box.

Now, for the volume, just picture cutting the sphere into lots of little polygons, and connect each of these to the center of the sphere to make a pyramid. A frustum of a cone is a cone whose top has been sliced off. I've defined x as the radius halfway up , and C as the circumference of that circle around the center of the ring; h is its vertical height and l its slant height. 54.Find the volume common to two spheres of radius r[/latex] with centers that are 2h[/latex] apart, as shown here.

For the following exercises, draw the region bounded by the curves. Then, use the disk method to find the volume when the region is rotated around the x[/latex]-axis. 10.A cone of radius r[/latex] and height h[/latex] has a smaller cone of radius r\text2[/latex] and height h\text2[/latex] removed from the top, as seen here. 1.Derive the formula for the volume of a sphere using the slicing method. The same general method applies, but you may have to visualize just how to describe the cross-sectional area of the volume.